ШАХМАТНЫЕ ЗАДАЧИ

Шахматные задачи

 

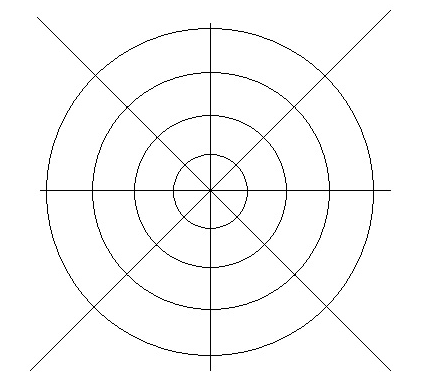
Фигуры на шахматной доске. Расстановки.

Задача 1. Ставим на доску слона (коня; ладью; ферзя). Сколько полей он бьет? ("Сколько мест на доске, куда, если поставишь пешку, ферзь сразу съест?" )

Задача 2. Какое максимальное количество клеток может бить слон (конь; ферзь; ладья)? На каких полях он должен для этого стоять?

Задача 3. Поставить слона (коня; ферзя) так, чтобы он бил ровно 11 (6, 27,. . . ) клеток.

И чуть сложнее:

Задача 4. Отметить (пешками, монетами и т.д.) все такие поля на доске, стоя на которых, слон (конь,. . . ) бьет ровно 9 (4, . . . ) клеток.

Количество клеток, конечно, можно и нужно варьировать - только при этом посматривать на доску (или даже прикинуть вопросы заранее), чтобы не промахнуться: не любое число годится. Можно обсудить этот факт с детьми, отсюда получится другое, более трудное задание, которое предполагает проведение целого исследования:

Задача 5. Какие числа можно задавать в задачах 3,4? Т.е. сколько клеток в принципе  может держать под ударом, например, конь? А сколько клеток он не может побить, как его ни ставь?

Задача 6. Расставить на доске как можно больше ладей так, чтобы ни одна не била (не могла съесть) другую. Почему больше нельзя? – доказать.

Вариант, может быть, чуть сложнее:

Задача 7. Ставим на доску несколько (5-7) ладей так, что ни одна не бьет другую. Задача – поставить остальные ладьи (как можно больше).

Задача 8. Более сложные варианты задачи 6: расставить как можно больше королей; слонов; ферзей; коней так, чтобы ни один из них не бил другого. Доказать, что больше поставить нельзя.

Задача 9. Расставить как можно меньше слонов (ферзей, коней) так, чтобы они били все свободные поля доски (и не били друг друга). Сколько слонов (ферзей, коней) получилось?

Заметим, что для ладей ответ тривиален (можно задавать эту задачу начинающим).

Задача 10. Расставить на шахматной доске шашки так, чтобы нигде нельзя было положить листок бумаги размером в 2 клетки. (Т.е. чтобы не было рядом двух пустых клеток.) Использовать как можно меньше шашек.

Вариант: то же самое с листком бумаги в 3 клетки. Или – с квадратным листком 2x2 клетки. Можно играть много раз и запоминать количество использованных шашек – пока не найдется оптимальная расстановка. Эту задачу можно преподносить, например, как "анти-Морской бой" (сколько мин и как надо заранее расставить, чтобы противник не смог поставить ни одного корабля?) или как борьбу старухи Шапокляк против создания в скверике какой-нибудь детской площадки.

И в заключение этого параграфа – несложные задачи на расстановку, вовсе не использующие шахматную доску:

Задача 11. На листе бумаги начерчены четыре концентрических окружности, пересеченные четырьмя прямыми, проходящими через центр (рис.1). Расставить 8 пешек так, чтобы на каждой окружности и на каждой прямой было по 2 пешки.

Эта классическая задача на расстановки тоже допускает усложнения: попроще – может
быть задано сразу после решения 11 как контрольный вопрос:

Задача 12. На том же поле и с теми же условиями расставить теперь 9, 10, 11 пешек. . .

. . . и посложнее – серьезная комбинаторная задача-исследование:

Задача 13. Сколько существует разных способов расставить пешки в задаче 11?

Рис. 1. Поле для задачи 11.

Задачу 11 можно преподнести и не в шахматном антураже, а, например, как историю про меткого лучника Вильгельма Телля, у которого злопыхатели поломали половину стрел, а он все-таки поразил каждую цель двумя стрелами.

Раз уж зашла речь про расстановки, упомянем здесь похожую и тоже классическую задачу про расстановку стульев в пустой комнате. В интересном для детей оформлении она выглядит примерно так:

Задача 14. Одна принцесса, собираясь замуж, решила проверить ум своих женихов. Она пригласила одного из них в прямоугольную (или квадратную) залу и попросила, пока он ее ждет, расставить у стен 4 кресла так, чтобы вдоль каждой стены стояло по 2 кресла. Нужно помочь жениху!

В другой раз (или со следующим женихом) то же повторилось с пятью (шестью, семью) креслами.

Странно, но дети, решив задачу для 4 кресел, часто затрудняются добавить пятое. Еще один психологический барьер стоит между 6 и 7 креслами. Можно, наоборот, начинать с восьми кресел, и по одному убирать их.

В шахматных терминах эта задача, очевидно, звучит так:

Задача 15. Расставьте 4 (5,6,7,8) пешек вдоль края доски так, чтобы вдоль каждой стороны стояло 2 пешки.

Далее:

Передвижение фигур

Задачи на четность