|
Обучение |
ГРАФЫ И РОДОСЛОВНЫЕ
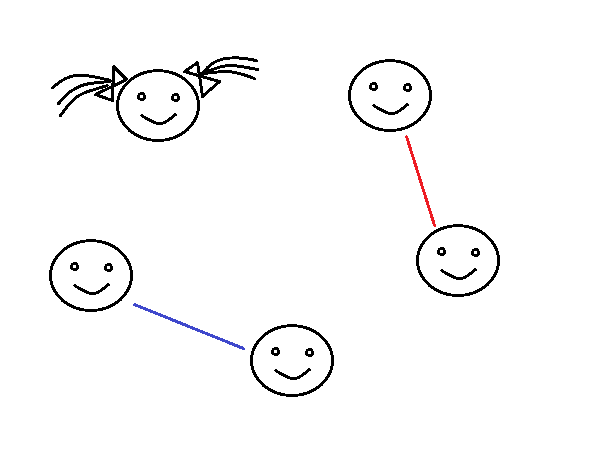
Разные задачи с графами (уровни 1-3). Здесь собраны разные задачи, знакомящие с идеей графов. Самые простые не требуют ни умения считать, ни знания букв. Часть из более сложных задач связаны с темой "Комбинаторика некоторые - использует идею делимости. Если решить задачу никак не получается – подумайте, может быть, удастся доказать, что это невозможно? Уровень 1. Задача 1. Взрослый рисует на листе бумаги 2 красные и 3 синие (например) точки (подальше друг от друга, никакие три не на одной прямой). Соединить линиями все красные точки со всеми синими. Сколько получилось линий? Число точек, конечно, можно и нужно варьировать. Эта задача - еще одна иллюстрация к понятию умножения для тех детей, кто это понятие уже знает. (То, что количества точек перемножаются, ребенок должен заметить сам, не спешите указывать на это.) Для более маленьких детей это будет упражнением на внимательность, на твердость руки и на счет. А заодно и подготовка к умножению. Задача 2. В семье два братика и две сестрички. Нарисуй эту семью (только лица, девочки - с косичками или бантами, мальчикам можно рисовать короткие волосики; в первый раз, скорее всего, нужно будет помочь) и проведи синие линии между братьями, красные - между сестрами и зеленые - от брата к сестре. Если дети маленькие, можно начать с семьи из двух человек и постепенно усложнять задачу. Задача 3. А теперь некоторые линии уже нарисованы, но неизвестно, кто тут мальчик, а кто - девочка (рис. 1). Нужно догадаться и дорисовать лица и линии.
Рис. 1: Кто здесь брат, кто сестра? Красные линии - между сестрами, синие - между братьями, зеленые - между братом и сестрой. Если ребенку эти задачи даются нелегко, нарисуйте ему еще несколько таких же. Задача 4. Игры со схемой метро (например, московского) или схемами разветвленных железных или автомобильных дорог. Как можно проехать от Сокольников до Бауманской? Как выбрать маршрут, чтобы проехать наименьшее число остановок? А чтобы было как можно меньше пересадок? А какой путь самый короткий, если учесть, что пересадка занимает примерно то же время, что один прогон между станциями? Задача 5. На бумаге нарисованы 8 точек, лежащих приблизительно на окружности. Соединить их линиями (т.е. нарисовать граф) так, чтобы их каждой точки выходило 3 линии. Для маленьких детей можно упростить задачу, нарисовав 6 или даже 4 точки. "Петли" , ведущие их точки в нее же саму, запрещены. Задача 6. Раскрасить линии графа из задачи 5 тремя цветами так, чтобы из каждой вершины (т.е. точки) выходили линии трех разных цветов. У задачи 5 много разных решений, так что этих задач-раскрасок можно задать несколько. Задача 7. 12 подружек стоят в кружок и играют в мяч (рис.2). Каждая кидает мяч своей соседке через одну (с любой стороны). Соединить линиями тех, кто может кинуть друг другу мяч (это все возможные "пути" мяча). Если в начале игры мяч у Ани, через сколько перебрасываний он может попасть к Яне? Задача 8. То же самое, если каждая девочка может кидать мяч своим соседкам через две? Задача 9. Все то же самое, если девочек 13.
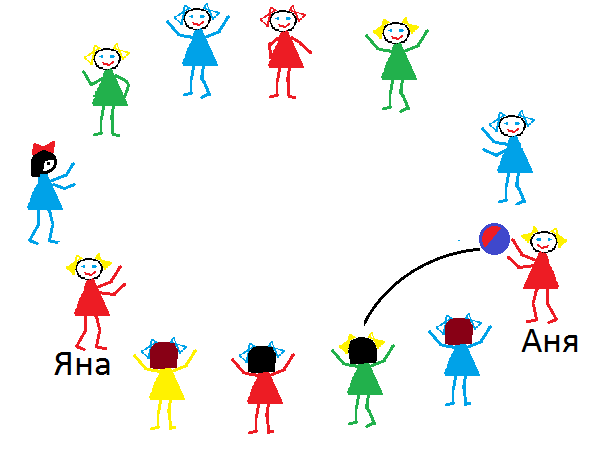
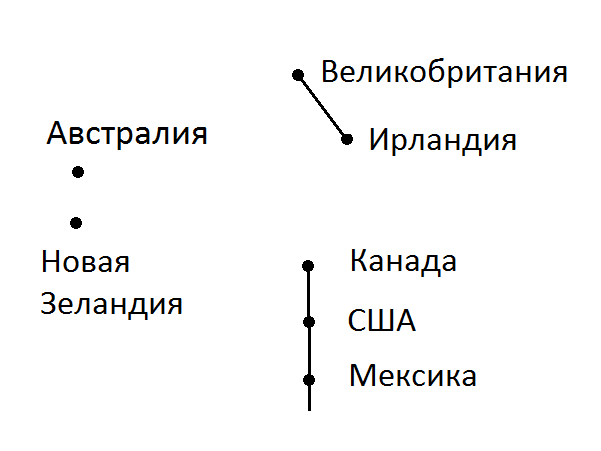
Рис. 2: Девочки с мячом. Продолжить траекторию мяча. Уровень 2 Задача 10. У двух подружек по три котенка, у каждого котенка по 2 хозяйки. Нарисуйте всю эту компанию и проведите линии от каждой хозяйки к каждому ее питомцу. Усложнения этой задачи: А если подружек четверо? А если трое? А если подружек десять - сколько тогда котят? Задача 11. На листе бумаги нарисованы 7 точек. Соединить их линиями (т.е. нарисовать граф) так, чтобы их каждой точки выходило 3 линии. Задача 12. Политический граф континента или острова - это граф, на котором точками обозначены страны, а линиями соединены такие пары стран, у которых есть общая сухопутная граница. Взаимное расположение точек (выше-ниже, левее-правее) неважно. Примеры графов Австралии и Тасмании, Новой Зеландии, Великобритании и Ирландии, Северной Америки (севернее тропика) показаны на рис.3. Нарисовать графы: 1) Южной Америки, 2) Азии, 3)Африки, 4) Европы.
Рис. 3: Примеры политических графов. Австралия и Тасмания – одно государство, одна точка; сухопутной границы с Новой Зеландией (два острова - одно государство) нет. Между Великобританией и Ирландией есть сухопутная граница, т.к. государство Великобритания занимает часть острова Ирландия. Задача 13. Знаменитый сыщик Шерлок Холмс составляет схему преступной сети Лондона. Каждый из трех всемирно известных лондонских преступных авторитетов (красные точки на схеме Холмса) имеет в подчинении четырех крупных бандитов (синие точки), а у каждого из этих последних - по 3 агента. Кроме того, каждому криминальному авторитету непосредственно служат еще по 3 агента. Каждый агент непосредственно связан с тремя "покровителями" , а каждый крупный бандит - с двумя. Ни один агент не знаком более чем с одним из трех крупнейших преступников. Но при этом каждый агент прямо или косвенно работает на всех троих. Нарисуйте схему, подходящую под эти условия.
Уровень 3. Задача 14. Все как в задаче 13, но есть еще одно дополнительное условие: у любых двух агентов может быть не более одного общего "покровителя" . |