|
Обучение |
КОМБИНАТОРИКА
Сосчитать пути (уровни 1-2). Во всех задачах на этой странице вопрос один и тот же: сколькими путями можно добраться из точки A в точку B? Возвращаться в точку, в которой уже был (т.е. проходить замкнутую петлю) – запрещается. Умение решать эти задачи делится на два этапа: на первом Ваш ученик понимает, что от него требуется, и считает варианты, обводя их по очереди карандашом. (Можно предложить ему для этой цели цветные карандаши, каждый маршрут – своим цветом. Если ребенок совсем не знает порядковый счет, он может только рисовать пути, а считать будет взрослый.) Этот этап полезен, хотя и несколько однообразен. Второй этап состоит в обобщении – умении посчитать варианты, не перечисляя их. Этому не нужно учить – ученик должен заметить это сам. Но нужно набрать достаточно опыта, а еще нужно как минимум понимать смысл умножения и знать начало таблицы умножения. Уровень 1 Начинаем с самых простых задач:
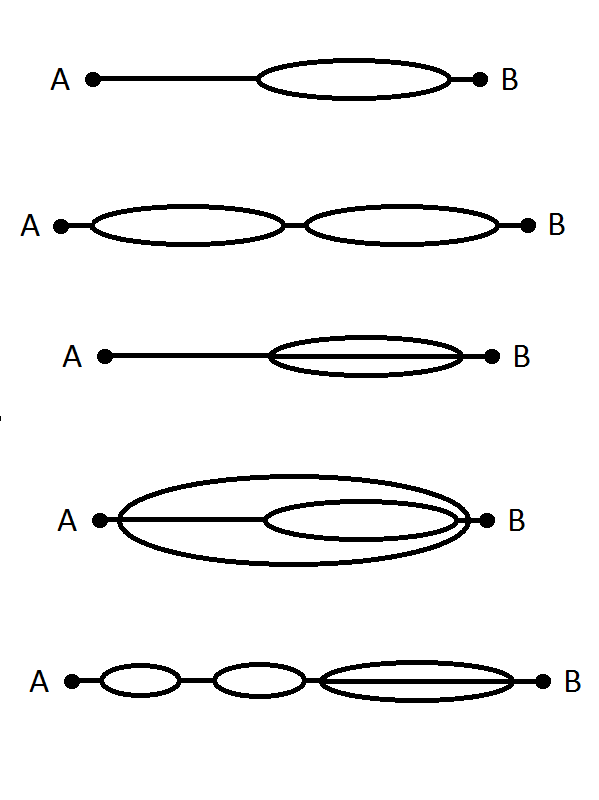
Рис. 1: Сколькими разными путями можно добраться из точки A в точку B? Возвращаться в точку, в которой уже был, нельзя. А вот картинки посложнее - рис. 2:
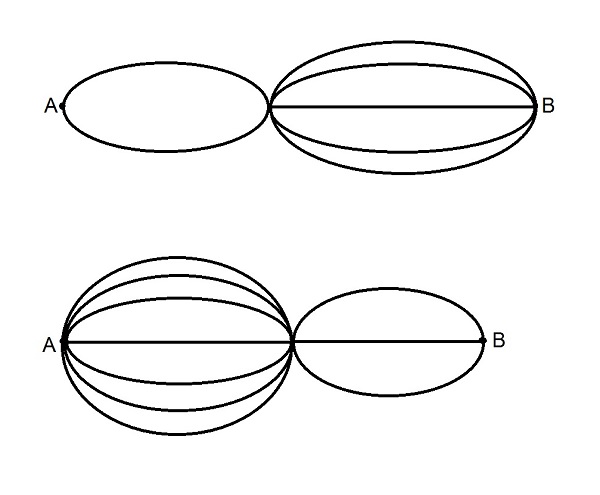
Рис. 2: Сколько разных путей из A в B? Ни одну точку нельзя проходить дважды. Таких задач, возможно, потребуется довольно много. Количество развилок и дорог нужно увеличивать постепенно. Не стоит давать подряд больше двух-трех картинок – а то может надоесть. Когда опыт накопится, можно попытаться подтолкнуть ученика к его обобщению. Уровень 2 Задача 1. Как сосчитать число путей из A в B на рис. 2, не перечисляя (не обводя) их все? Задача 2. Из деревни Петухи в деревню Кукушечки можно пройти 6-ю разными дорожками и тропинками, а из Кукушечек в село Жаворонки ведут 5 дорог. Петя живет в Петухах, а учится – в Жаворонках. Он решил каждый день ходить в школу новым путем. Через сколько дней он сходит в школу в последний раз? (А может быть, это был не Петя, а Красная Шапочка, которая ходила к бабушке в гости разными путями, чтобы сбить с толку Волка.)
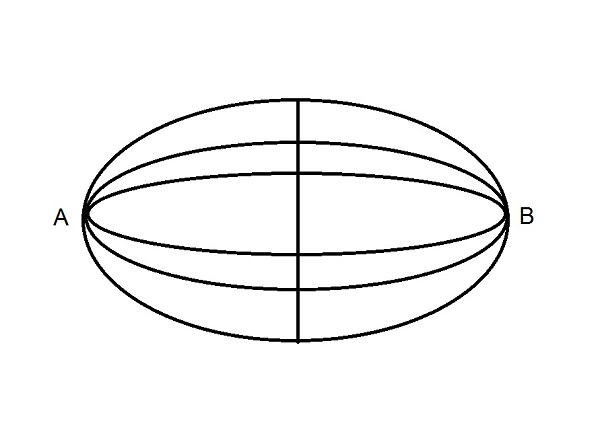
Рис. 3: А как быть с такой картинкой? Если ребенок, которому "давно пора все понять по-прежнему перебирает все варианты вместо того, чтобы просто сосчитать их – можно попытаться воздействовать на него, доведя ситуацию до абсурда: Задача 3. Из А в В ведет одна дорога, а из В в С – 100. Сколько возможных путей из A в C? А теперь из А в В построили вторую дорогу. Сколько теперь стало способов добраться из A в C? А если из A в B – 10 дорог? Если такие задачи решать научились, можно начать составлять их комбинации (рис. 4).
Рис. 4: Разветвленная сеть дорог. Можно обыгрывать эти картинки – например, сказать, что это такой способ зашифровать секретное число. Тогда естественным образом возникает, например, такая задача: Задача 4. Нарисуйте сами такую сеть дорог, чтобы A в B было 16 путей. Или такая: Задача 5. Из A в B можно было пройти 12-ю разными способами. Но потом достроили еще один участок дороги, и возможных путей стало 15. Как теперь выглядит схема дорог в этой местности? Уровень 3 А бывают ситуации, когда придумать порядок, в котором пересчитывать пути – непросто:
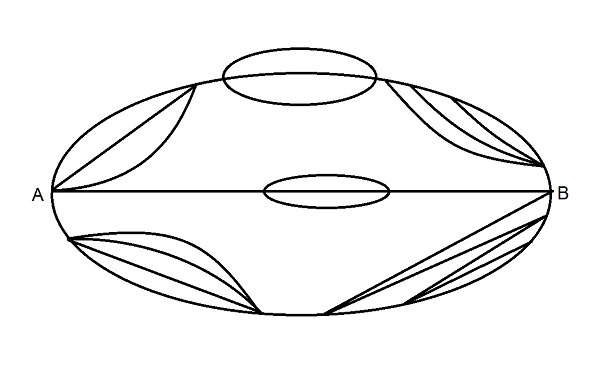
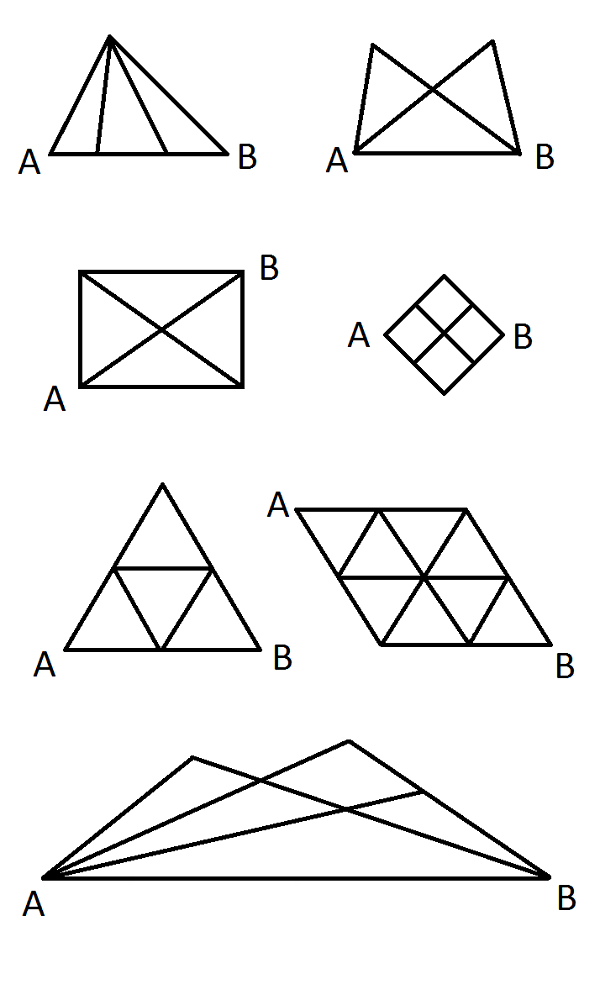
Рис. 5: Некоторые из этих картинок можно перерисовать так, чтобы они стали похожи на рис. 2 или 4, а некоторые – нет. Для каждой из таких картинок придется отдельно придумывать, в каком порядке пересчитывать пути. Далее: Разные задачи по комбинаторике |