РАЗРЕЗАНИЕ

Разрезание многоугольников одной прямой

 

Деление на неравные части (уровни 2-3).

В разделе "Разрезание многоугольников"мы делили фигуры на части одним разрезом – здесь будем делать два или три разреза. Задачи такого типа встречаются в задачниках и на олимпиадах. Форма получающихся кусков при этом обычно неважна, но важно их количество. Не стоит, пожалуй, давать эти задачи совсем маленьким – и не только потому, что нужно уверенно считать в пределах десятка. Видимо, при недостаточном жизненном опыте трудно представить себе, как будет выглядеть картинка после проведения двух прямых; поэтому попытки решения в таких случаях выглядят как хаотические, без какого-либо понимания причин неудачи.

Уровень 2.

Задача 1 Разрезать квадратный (или круглый) торт тремя прямыми линиями на 7 частей. Части не должны быть равными!

Как ни странно, эта задача может вызывать трудности. Если она, наоборот, решилась сразу – можно проверить, не случаен ли успех, попросив разделить такой же торт на 6 частей. А на 5 (это, может быть, самое трудное)? От ребят постарше можно пытаться добиться объяснений, почему круг нельзя разрезать тремя линиями больше чем на 7 частей.

Классический, немного усложненный вариант этой задачи – на торте нарисованы 7 розочек, и разрезать надо так, чтобы на каждой части оказалось по одной (рис. 1). В других версиях это козы на капустном поле, ежики в лесу и т.д. Такие картинки легко сделать самому, начиная "от готового решения" . Розочки (или ежики) должны быть достаточно большими и почти касаться запланированных линий разреза, чтобы оставить поменьше свободы при их проведении.

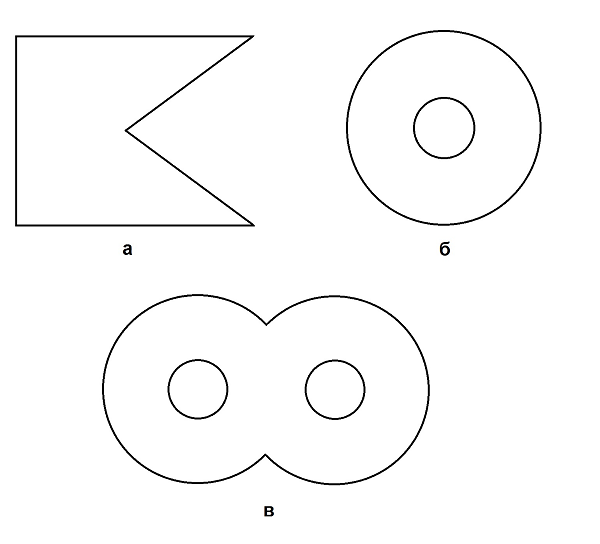
Рис. 1: Разрезать торт тремя прямыми линиями на 7 кусков так, чтобы в каждом куске было по розочке.

Задача 2 Разрезать флажок (рис. 2,а) двумя прямыми линиями на как можно большее число частей.

Вариации этой же задачи – разрезать толстую букву П (или Л), подкову или нарисованный валенок.

Рис. 2: Эти фигуры нужно разрезать двумя разрезами на максимальное возможное количество частей. Заметим, что ответ в задаче (в) изменится, если сделать "вырезы" более глубокими.

Если эти задачи удалось решить – это уже замечательно. Еще лучше, если удастся добиться какой-то рефлексии по поводу этого результата, какого-то объяснения, почему так получилось, "как ты рассуждал" . Неслучайность правильного ответа можно проверить, задав ту же задачу с бубликом (рис 2,б) или квадратом с дыркой, толстой восьмеркой (рис 2,в), фигурой с тремя дырками в ряд. Для всех этих фигур можно ставить вопрос и так:

Задача 3 На сколько кусков возможно разделить фигуру (из рис. 2, например), сделав 2 прямых разреза?

(Эта постановка - немного более общая, чем в предыдущей задаче: надо найти не только "оптимальный " способ, но и все возможные другие варианты.) В качестве подсказки можно указывать максимально возможное число частей. Сознательное решение таких задач предполагает понимание, что точку пересечения прямых надо выбирать внутри фигуры (это сразу дает 4 куска), а сами прямые ориентировать так, чтобы они прошли через как можно большее количество "дырок" причем новый кусок появится, если обе прямые пересекут одну и ту же дырку. Как всегда, конечно, ценно не сообщение ученику этой информации, а его собственная догадка. Поэтому если он, ни о чем не рассуждая, решает подбором – ну что ж, набирается опыта.

Уровень 3.

Задача 4 То же, что в задачах 2 или 3, но разрезов - три.

Еще один способ усложнить эти задачи - предлагать разрезать "кренделя" с большим количеством изгибов или дырок. Но не стоит этим очень увлекаться: если главный принцип уже понятен, это становится во многом упражнением на точное проведение прямых линий, а если еще непонятен - игрой "на везение" .

Еще один классический вид задач на разрезание – разрезать данную фигуру на заданное число частей и собрать из них другую фигуру. Сейчас они довольно редко встречаются – возможно, из-за их сложности. Здесь мы приводим несколько задач, использующих один общий прием; это – упрощенные версии задач из книги Кордемского.

Задача 5 В квадратном коврике 3м x 3м пришлось вырезать протертую середину 1м x 1м (рис. 3,а). Как разрезать этот ковер на 2 части (не обязательно прямой линией!) и сшить из них новый прямоугольный ковер?

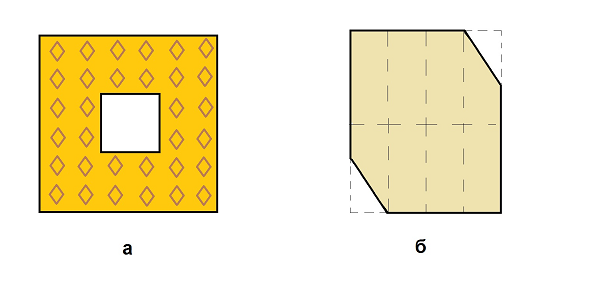
Рис. 3: Разрезание с последующей переклейкой: разделить на 2 части и сделать
прямоугольник.

Задача 6 Как из прямоугольной доски размером 9x4м собрать квадратную столешницу 6x6м, распилив ее всего на два куска?

Задача 7 А в этот раз нужно распилить на 2 части кусок фанеры с симметрично отрезанными углами (рис. 3,б; не обязательно пилить по прямой!) и сложить из этих частей прямоугольник.

Дополнительное упражнение – вычислить размеры полученного прямоугольника, считая размеры начального куска известными.

Далее:

Разбиение на клетчатой бумаге