|
Обучение |
КОМБИНАТОРИКА
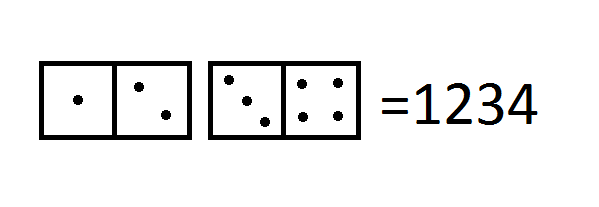
Разные задачи по комбинаторике Есть два разных способа решения этих задач. Один – детский – перебор всех возможных вариантов. Второй – взрослый – состоит в придумывании такого порядка перебора, что перечислять все комбинации уже не нужно: они распадаются на группы, число возможных комбинаций в каждой группе легко сосчитать. Пример: сколькими способами можно раздать десяти детям десять разных фруктов? Не станете же Вы перебирать все варианты. . . Однако до взрослого способа нужно еще дорасти. Для начала перебрать десяток вариантов в любом порядке, ничего не забыв и не повторяясь - уже достаточно сложная задача. Причем ее решение от умения считать не зависит. Первое время нужно брать совсем маленькие числа, чтобы число вариантов было не больше 5-6, и обязательно давать в руки "счетный материал" : годятся любые предметы, главное – чтобы их хватило для раскладывания всех комбинаций. Можно строить все возможные двухэтажные дома из разноцветных кубиков, можно собирать пары из разноцветных шариков, лоскутков или карандашей, можно выкладывать все возможные последовательности заданной длины из ложек и вилок или рублевых и десяти-рублевых монеток. . . Потом можно переходить от раскладывания цепочек к их рисованию. И только потом, когда дети будут уверенно находить все варианты и начнут сами их упорядочивать (сначала - все случаи с синим кружочком. . . ) – можно предложить им "угадывать" ответ, не перечисляя все случаи. И то, скорее всего, Вы встретите ожесточенное сопротивление: легче нарисовать 30 поездов с цветными вагончиками, чем придумать одну идею. В этом разделе задачи не упорядочены по сложности. Пока не найден общий принцип решения каждого типа задач, их сложность регулируется небольшим изменением количества цветов или длины составляемых комбинаций. Не берите много - количества вариантов очень быстро растут. Большие числа стоит давать только тогда, когда Вы хотите заставить учеников перейти наконец к "взрослой" схеме подсчета, а они все рисуют и рисуют все варианты. С чего начать Задача 1. У нас есть 3 фломастера. Рисуем цветочки: серединка одного цвета, лепестки другого. Нужно нарисовать как можно больше разных цветков. Задача 2. У Пети есть кубики трех цветов. Сколько разных трехэтажных домиков он сможет из них составить? А сколько из них трехцветных? Задача 3. На столе лежит горстка спичек, кучка одинаковых монеток и кучка шурупов (или, например, одинаковых пластилиновых шариков). Разложить эти предметы в ряды по 3 штуки так, чтобы ряды не повторялись. Сколько рядов можно сделать? Серия задач про поезда Задача 4. В депо есть вагоны двух разных цветов. Из них составляют поезда длиной в 5 вагонов, которые прицепляют к паровозу. Сколько разных поездов можно составить из одного белого и четырех синих вагонов? А из двух белых и трех синих? У этой задачи огромное множество вариантов различной сложности. Можно менять количество вагонов и цветов; если цветов больше двух, то можно делать трехцветные поезда, например: Задача 5. Сколько поездов можно составить из одного белого, одного желтого и трех синих вагонов? (Чем эта ситуация отличается от двух белых и трех синих?) А из одного белого, двух желтых и двух синих вагонов? С этими же вагонами есть еще и такая задача – для маленьких она сложнее, а для детей постарше, возможно, даже проще предыдущих: Задача 6. Сколько всего разных поездов можно составить из белых и синих вагонов? А если есть еще желтые вагоны? Заметим, что задача решается на самом деле ("по-взрослому" ) совсем не так, как предыдущие. Поэтому на этапе перехода от перебора к аналитическому решению ее стоит задавать отдельно. А можно составлять полностью разноцветные поезда: Задача 7. К празднику в депо завезли краску 5-ти разных цветов, и начальник депо решил составлять проезда, в которых все вагоны разных цветов. Сколько разных поездов он сможет составить? А сколько всего разных трехцветных поездов, если в депо есть вагоны пяти разных цветов? Другие сюжеты. Вместо вагонов и поездов могут быть лампочки в гирлянде, кирпичики от конструктора и построенные из них дома, пуговицы разных размеров и т.д. Ниже мы приводим примеры задач в другом антураже, многие из них (но не все) дублируют "вагонные" задачи. Если дети узнают уже решенную когда-то задачу в новом облике, а тем более если смогут объяснить, чем эти задачи похожи – это очень хорошо. Задача 8. Ира делает цепочки по 5 бусинок и вешает их маленькому брату на кроватку. Бусинки у нее двух цветов - желтые и голубые. Сколько разных цепочек с одной желтой бусинкой у нее может получиться? А с двумя? А с тремя? А с четырьмя? А с пятью? А если в каждой цепочке одна желтая бусина, одна красная, остальные голубые? Задача 9. Ключи. Есть 3 замка и 3 ключа к ним. Сколько (максимум) попыток нужно, чтобы выяснить, к какому замку какой ключ? А чтобы открыть все замки? (Это два разных вопроса, и ответы на них отличаются! Эту разницу полезно обсудить.) Как число замков, так и число ключей могут варьироваться от двух до, скажем, пяти, и совсем не обязательно, чтобы ключей и замков было поровну. Задача 10. Шахматный король идет по клетчатому полю из клетки A1 на клетку B5. (Он может ходить вперед-назад, направо- налево и по диагонали). Сколько у него способов пройти за наименьшее число шагов? (т.е. сколько кратчайших путей?) А если он не будет ходить по диагонали? Усложнение задачи: нужно попасть на C 5. Задача 11. (Уровень 3) А сколько у этого короля вообще способов попасть (не обязательно коротким путем) из A1 в B5, если он не может возвращаться в клетку, в которой уже побывал? (т.е. его путь не должен содержать замкнутых петель). Это достаточно сложная задача, даже если запретить ходить по диагонали. Задача 12. Есть кубики 4 цветов. Сколько разных 2 этажных домов можно из них построить? А трехэтажных домов с разноцветными этажами? А если бы было 100 разных цветов? Задача 13. Флаги многих стран, как и флаг России, состоят из трех горизонтальных цветных полос. Сколько таких флагов можно нарисовать, имея 6 красок? Допускаются полосы одного цвета (в том числе и соседние). (А можно и запретить делать соседние полосы одинаковыми, и это будет другая задача.) Задача 14. В детсаду всем детям раздали по листу бумаги, на каждом были нарисованы круг, квадрат, треугольник и звездочка. Дети раскрасили эти фигуры, причем у них были фломастеры только трех (или четырех) цветов, а каждая фигура была раскрашена каким-то одним цветом. Оказалось, что у всех рисунки разные. Сколько (самое большее) детей могло быть в этом саду? Задача 15. Сколько всего двузначных чисел? Трехзначных? Двузначных с разными цифрами? Двузначных, у которых первая цифра больше второй? Трехзначных, у которых самая большая цифра – последняя? Задача 16. Гном спрятал под горой свои сокровища. Известно, что у него были алмазы, топазы и изумруды, а в каждый клад он прятал по 7 камней, и все клады разные. Сколько всего под горой может быть кладов? Задача 17. Король распорядился, чтобы на следующем балу все пары были одеты по-разному. При дворе разрешены только однотонные платья и фраки 5-ти цветов. Сколько пар прибудет на бал? (Король согласен, что дама в желтом, кавалер в красном и кавалер в желтом, дама в красном – это две разных пары.) Задача 18. А на следующий бал король еще и запретил одноцветные пары (дама и кавалер в одежде одинакового цвета), сочтя их слишком скучными. Сколько цветов нужно разрешить, чтобы на бал смогли прийти 200 человек? Задача 19. Сколькими разными способами можно усадить 4 человека за квадратный стол? Конфигурации, которые отличаются друг от друга поворотом всего стола как целого, считаются одинаковыми. (А если такие конфигурации считать разными, т.е. если, например, стол стоит возле окна и важно, кто сидит к нему лицом – опять получается новая задача.) Задача 20. Сколько имен можно составить, переставляя слоги в имени Кокованя? (по сказке П. Бажова "Серебряное копытце" ) Здесь любая комбинация слогов считается именем. Чем, собственно, имя Някокова хуже, чем Кокованя? Задача 21. Сколько способов переставить буквы в слове АТАКА? КАБАК? КАБАН? (То, что получается, не обязано быть осмысленным словом.) Задача 22. Далеко на севере Капелла плещет семицветным огоньком... /С. Есенин/ Настина задача о звезде. Двойная затменно-переменная звезда может светить тремя способами: мы видим обе звезды, только первую (а вторая за ней) и, наоборот, только вторую – если звезды неодинаковы, суммарная яркость во всех трех случаях будет разной. А сколько способов светить у тройной звезды? Задача 23. Игра СЕТ – это набор карточек, отличающихся друг от друга четырьмя признаками (цветом, формой, количеством и способом закрашивания нарисованных на них деталей); по каждому признаку есть 3 варианта (3 цвета, 3 формы. . . ), в наборе есть все возможные сочетания этих признаков. Сколько карточек в наборе игры СЕТ? Конечно, эту задачу стоит задавать, если дома есть эта игра или, например, логические блоки Дьенеша – вообще любая игра, где представлены все сочетания двух-четырех признаков. При этом надо сначала достать игру, рассмотреть, обсудить и только тогда задать вопрос (но не давать считать карточки). В упрощенном варианте задачи можно убрать один признак, например, считать только те карточки, которые раскрашены сплошной заливкой. Если их сосчитать удалось, можно считать уже все карточки. Задача 24. Географическая. На глобусе меридианы нарисованы через каждые 15 градусов, параллели – через каждые 10 градусов. На сколько частей разделена этими линиями поверхность глобуса? Задача 25. "Веселые старты" . (Уровень 2-3) Сколькими способами можно разделить 8 человек на 2 равные команды? А 9 человек на 3 команды? Задача 26. (По мотивам задачи из Олимпиады 2x2) Выкладываем числа доминошками: например, из двух доминошек складывается четырехзначное число - см. рис. 1. Какое самое большое число можно выложить, используя один стандартный комплект домино? Сколько разных четырехзначных чисел можно выложить, используя не более одного стандартного комплекта домино для каждого числа? А шестизначных?
Рис. 1: Как из костяшек домино сложить число. . . . и немного о графах В заключение – еще несколько задач, объединенных общей идеей (уровень 2-3). Эти задачи одновременно относятся и к теме "Графы" . Задача 27. У мамы 4 дочки, у каждой 3 котенка, у каждого котенка две хозяйки. Сколько всего котят? Задача 28. Туристы устраивали игру для детей. Они выбрали 12 деревьев и привязали к ним концы веревочек – в середине получилась веревочная путаница. К каждому дереву оказалось привязано по 5 веревок. А сколько всего веревок потребовалось? Эти задачи тоже можно решить, нарисовав картинку (как это и предлагается в "Графах" ) – особенно если вместо 12 взять число поменьше. Но картинка не будет доказательством правильности ответа, а только догадкой – мы же не знаем, какие именно деревья были связаны между собой, и какой котенок был у какой девочки. Нужно придумать решение, которое обходится без картинки, этим решением мы докажем, что как веревочки ни привязывай, их в любом случае понадобится одно и то же число. |